L'électricité
I - Le courant électrique
⇨ Le courant électrique est créé par la mise en mouvement de porteurs de charge. Dans un matériau conducteur c'est un déplacement d'électrons libres. Dans une solution aqueuse c'est un déplacement d'ions (cations et anions).
⇨ Par convention, le courant circule de la borne positive vers la borne négative, à l'exterieur du générateur. Les électrons circulent dans le sens opposé. Sur le schéma d'un circuit, le sens de circulation du courant est représenté par une flèche, posée sur le fil conducteur et notée I ou i (ce qui indique l'intensité du courant électrique) :
\[ \bbox[yellow, 4px, border:1px solid red] { I=\dfrac{Q}{Δt} } \]⇨ L'intensité du courant électrique représente le nombre d'électrons qui traversent la section du fil pendant une seconde (c'est un flux d'électrons). On mesure l'intensité du courant avec un ampèremètre branché en série, ou avec une pince ampèremétrique. L'intensité du courant s'exprime en ampère (A).
II - La tension électrique
⇨ La tension électrique entre les bornes d'une pile résulte de la différence du nombre d'électrons entre ces bornes. On parle de potentiel électrique. la borne positive à moins d'électrons que la borne négative et peut potentiellement en accueillir plus ! Le potentiel de la borne positive est supérieur à celui de la borne négative. La tension électrique est une différence de potentiel (ddp) :
\[ \bbox[yellow, 4px, border:1px solid red] { U_{AB}=V_A - V_B } \]⇨ La tension électrique est réprésentée par une flèche à coté d'un dipôle. Si une tension est positive, la pointe flèche indique vers la borne "positive" (le potentiel le plus grand) et la queue de la flèche indique la borne "négative" (le potentiel le plus petit).
⇨ La tension électrique se mesure avec un voltmètre branché en parallèle (= en dérivation), entre les deux bornes d'un dipôle.
III - La convention générateur et la convention récepteur
Lorsqu'on étudie un circuit électrique, on utilise des flèches pour représenter le courant et la tension.
Chaque dipôle a donc deux flèches (une pour le courant, l'autre pour la tension).
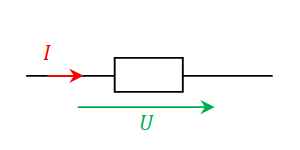
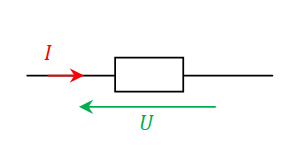
Si on pense que le dipole est un générateur on place les deux flèches dans le même sens (convention générateur). Si on pense que le dipôle est un récepteur on place les flèches en sens opposé (convention récepteur).
Pour un générateur : si la puissance fournie est positive alors c'est vraiment un générateur. Si la puissance fournie est négative alors c'est en réalité un récepteur.
Pour un récepteur : si la puissance reçue est positive alors c'est vraiment un récepteur. Si la puissance reçue est négative alors c'est en réalité un générateur.
| Convention générateur | Convention récepteur |
|
|
|
| Si on pense que le dipôle étudié est un générateurs, on adopte la convention générateur : la flèche de tension est dans le même sens que la flèche du courant. | Si on pense que le dipôle étudié est un récepteur, on adopte la convention récepteur : la flèche de tension et la flèche du courant sont en sens inverse. |
| La puissance fournie : Pfournie = U×I | La puissance reçue : Preçue = U×I |
| • Si Pfournie > 0 alors le dipôle fonctionne réellement comme un générateur. | • Si Preçue > 0 alors le dipôle fonctionne réellement comme un récepteur. |
| • Si Pfournie < 0 alors le dipôle fonctionne en fait comme un récepteur. | • Si Preçue < 0 alors le dipôle fonctionne en fait comme un générateur. |
IV - Loi des nœuds et loi des mailles en régime continu
| Loi de nœuds : la somme algébrique des courants en un nœud est nulle. | Loi des mailles : la somme algébrique des tensions le long d'une maille est nulle. |
|
|
|
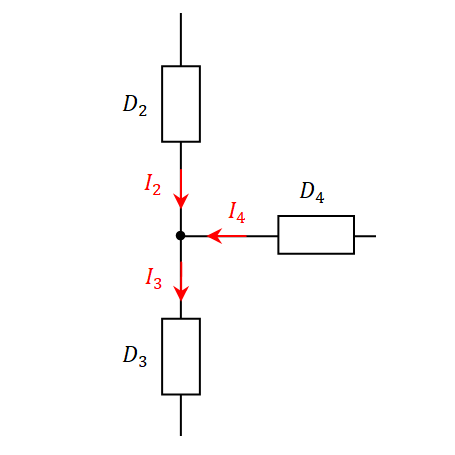
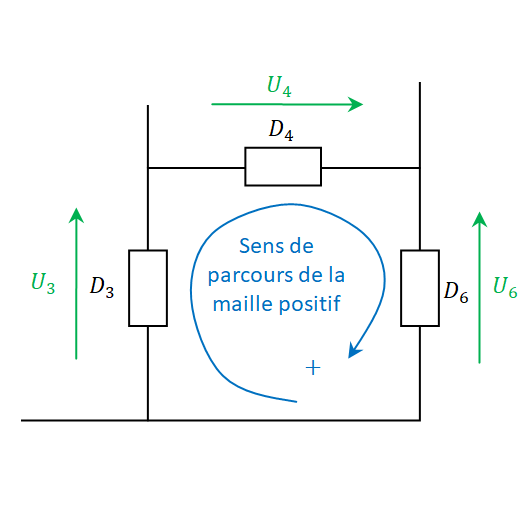
| Les courants qui arrivent au noeud sont comptés positivement. Ceux qui en partent sont comptés négativement : | Les tensions qui sont dans le sens de parcours de la maille sont comptées positivement. Celles en sens inverse sont comptées négativement : |
| +I2 +I4 −I3 = 0 | +U3 +U4 −U6 = 0 |
VI - La loi d'Ohm
Aux bornes d'un dipôle ohmique de résistance R, la tension électrique U est proportionnelle à l'intensité I du courant qui le traverse.
\[ \bbox[yellow, 4px, border:1px solid red] { U=R \times I } \]Le coefficient de proportionnalité entre la tension U et l'intensité I s'appelle la résistance électrique. On la note \(R\) et elle s'exprime en ohm (symbole : \(Ω\)) [lire "oméga", lettre majuscule grecque].
[remarque : graphiquement on peut dire qu'il y a proportionnalité lorsque la courbe obtenue est :
- une droite
- et que la droite passe par l'origine du repère.
Le coefficient proportionnalité est alors égale au coefficient directeur de la droite]
L'énergie électrique
I - Le régime sinusoïdal
⇨ On dit qu'un circuit électrique fonctionne en régime sinusoïdal si les tensions et l'intensité des courants qui le parcours sont sinusoïdaux. C'est-à-dire que leurs évolution au cours du temps peuvent être modélisée par une fonction sinusoïdale (fonction sinus ou cosinus).
En régime sinusoïdal, on constate généralement, pour un dipôle, un décallage entre la courbe de représentant l'évolution de la tension et la courbe représentant l'évolution de l'intensité du courant. Mathématiquement, ce décallage est modélisé par l'ajout d'un terme dans la phase de la tension ou du courant, on parle alors de déphasage. On note \(φ\) ce déphasage :
\[ { u(t)=U_{max}×\sin(ωt) } \]D'autre part,
\[ { i(t)=I_{max}×\sin(ωt+φ) } \]Aux bornes de ce dipôle, la puissance instantanée s'exprime donc par la relation :
\[ { p(t)=u(t)×i(t) } \]II - Puissance active et puissance apparente
⇨ La puissance active, notée \(P\), est la valeur moyenne de la puissance instantanée. C'est cette puissance qui produit réellement un travail. C'est elle qui est réllement active lors de la transmission de l'énergie.
\[ \bbox[yellow, 4px, border:1px solid red] { P=P_{moy} } \]Le calcul de la valeur moyenne de la puissance instantanée en régime sinusoïdal permet de montrer que :
\[ { P=\frac{1}{T}\int_{0}^{T}p(t)dt=UI\cosφ } \]⇨ La valeur \(\cosφ\) étant comprise entre \(-1\) et \(1\), la plus grande valeur de puissance active pouvant apparaître au cours du fonctionnement d'une installation électrique, est le produit \(U×I\). Cette valeur maximale de la puissance active est appelée puissance apparante. Elle est notée \(S\) :
\[ \bbox[yellow, 4px, border:1px solid red] { S=U×I } \]La puissance apparante permet le dimensionnement une installation ou un équipement électrique ; c'est-à-dire de choisir le diamètre des cables électriques à mettre en place, la puissance nécessaire de la source d'énergie électrique du réseau, ou les dispositifs de sécurité...
⇨ Le facteur de puissance caractérise la puissance transmise par une installation électrique en la comparant à la valeur moyenne maximale qu'elle pourrait transmettre. Le facteur de puissance se définit par la relation mathématique :
\[ \bbox[yellow, 4px, border:1px solid red] { k=\dfrac{P}{S} } \]Remarque. Pour les appareils de puissance supérieur à \(25 W\), la norme EN 6100-3-2 exige d'avoir un facteur de puissance minimal de \(0,9\).
Plus le facteur de puissance est proche de \(1\), meilleure est l'installation.
En régime sinusoïdal, le facteur de puissance dépend du déphasage entre la tension et l'intensité du courant : \(k=\cosφ\).